Macs Based on Hash Function (HMAC)

 It is a technique that combines public key, Private Key, and a hash into  a mix hackers can't unpack. 

HMAC Algorithm : 

The keywords to remember : 

H = Embedded hash function (e.g.; MD5, SHA-1, RIPEMO-160)

IV = Initial value Input to hash function.

M = Message Input to HMAC (including the padding specified in the embedded hash function)

Yi = ith block if M, 0<=i<=(L-1)

L = number of blocks in M

b = Number of bits in a block.

n = Length of hash code produced by embedded hash function.

K = secret key; recommended length >=n; if key length is greater then b, then key is input to the      hash function to produce an n-bit key.

K+ = K padded with zeros on the left so that the result is b bit in length

ipad = 00110110 (36 in Hexadecimal) repeated b/8 times.

opad = 01011100 (5C in Hexadecimal) repeated b/8 times.

The HMAC can be expressed as : 

HMAC(K,M) = H[(K+ XOR opad) || H[(K+ xor ipad) || M]] 

Figure 1 explains the Structure of HMAC


Fig: 1. HMAC Structure

Step 1. Make the Length of K+ equal to b. 
    . if length of  K+<b; add 0 bit required to left of k.
    . if the length of K+=b; in this case, we do not take any action, and proceed to step 2. 
    . if the length of K+>b ;  we need to trim k, for this, we pass k through the message digest algorithm          selected for this particular instance of HMAC.

Fig. 2: Procedure of Step 1

Step 2. Xor with K+ ipad to produce Si. 
    . Xor K+ (the output of step 1) and ipad to produce a variable called Si. 
    . Equation : K+ xor ipad  = si


Fig. 3: Procedure of Step 2.

Step 3. Append original message M to Si.
    . Take the original message M and simplify append it to the end of Si.
    . Equation : [(K+ xor ipad) || M] = Si || M



Fig. 4: Procedure of Step 3. 

Step 4. Apply Message Digest algorithm.

    . The selected message digest (e.g. MD5,SHA-1, etc) is applied to the output of step 3. 

    . Equation : H[(K+ xor ipad) || M] = H(Si || M)


Fig. 5: Procedure of Step 4. 

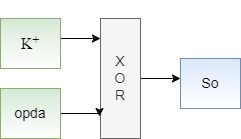
Step 5. Xor K+ with opad to produce So.

    . K+ Xor (the output of step 1) with opad to produce a variable called So.
    . Equation : K+ xor opad = So


Fig. 6: Procedure of Step 5.
Step 6. Append H to So.
    . Append the message digest calculated in step 4 to the end of So. 
    . Equation : (K+ xor opad) || H[(K+ xor ipad) || M] = So || H(Si || M)


Fig. 7: Procedure of Step 6.

Step 7. Apply Message digest Algorithm.
    . The selected message digest (e.g. MD5, SHA-1,etc) is applied to the output of step 6. 
    .  Finally, we got MAC. 
    . Equation : HMAC(K,M) = H[(K+ xor opad) || H[(K+ xor ipad) || M]]


Fig. 8: Procedure of Step 7. 

Efficient Implementation : 
A more efficient implementation is possible. Two quantities are precomputed. 
    f(IV, (K+ xor ipad)
    f(IV, (K+ xor opad)


Fig. 9: Efficient Implementation of HMAC

%3CmxGraphModel%3E%3Croot%3E%3CmxCell%20id%3D%220%22%2F%3E%3CmxCell%20id%3D%221%22%20parent%3D%220%22%2F%3E%3CmxCell%20id%3D%222%22%20value%3D%22%22%20style%3D%22shape%3Dtable%3BstartSize%3D0%3Bcontainer%3D1%3Bcollapsible%3D0%3BchildLayout%3DtableLayout%3BfontSize%3D14%3BgradientColor%3D%23ffffff%3B%22%20vertex%3D%221%22%20parent%3D%221%22%3E%3CmxGeometry%20x%3D%22390%22%20y%3D%22450%22%20width%3D%2260%22%20height%3D%2240%22%20as%3D%22geometry%22%2F%3E%3C%2FmxCell%3E%3CmxCell%20id%3D%223%22%20value%3D%22%22%20style%3D%22shape%3DpartialRectangle%3Bcollapsible%3D0%3BdropTarget%3D0%3BpointerEvents%3D0%3BfillColor%3Dnone%3Btop%3D0%3Bleft%3D0%3Bbottom%3D0%3Bright%3D0%3Bpoints%3D%5B%5B0%2C0.5%5D%2C%5B1%2C0.5%5D%5D%3BportConstraint%3Deastwest%3BfontSize%3D14%3B%22%20vertex%3D%221%22%20parent%3D%222%22%3E%3CmxGeometry%20width%3D%2260%22%20height%3D%2240%22%20as%3D%22geometry%22%2F%3E%3C%2FmxCell%3E%3CmxCell%20id%3D%224%22%20value%3D%22%22%20style%3D%22shape%3DpartialRectangle%3Bhtml%3D1%3BwhiteSpace%3Dwrap%3Bconnectable%3D0%3Boverflow%3Dhidden%3BfillColor%3Dnone%3Btop%3D0%3Bleft%3D0%3Bbottom%3D0%3Bright%3D0%3BpointerEvents%3D1%3BfontSize%3D14%3B%22%20vertex%3D%221%22%20parent%3D%223%22%3E%3CmxGeometry%20width%3D%2260%22%20height%3D%2240%22%20as%3D%22geometry%22%3E%3CmxRectangle%20width%3D%2260%22%20height%3D%2240%22%20as%3D%22alternateBounds%22%2F%3E%3C%2FmxGeometry%3E%3C%2FmxCell%3E%3C%2Froot%3E%3C%2FmxGraphModel%3Eb
Note 1: Please study the below Table regarding the advantages and limitations of HMACs. ☺

Advantages:

1      HMAC is faster to compute and verify digital signature because they use hash function rather than public key.

2      HMACs can be used in some cases where the public key cryptography is prohibited.

3       HMACs are much smaller than digital signature.

 

Drawbacks:

1       Key exchange is main issue, so can’t prevent against replay.

2       HMAC cannot be used if the number of receiver is greater than one.

3       If multiple parties share the same symmetric key. How does a receiver know that the message was prepared and sent by the sender.

 

*************************************************************************************************************

Comments

Post a Comment

Popular posts from this blog

Homomorphic Encryption: A Basic Idea

Image
Homomorphic encryption has the same aim as other encryption-decryption mechanisms: maintaining confidentiality, security, privacy, etc.  In this blog, we will see homomorphic encryption and its type.  Homomorphic Encryption (HE):  It is an encryption that computes operations over encrypted data without decrypting it (or without the need for a secret key).  Mathematically speaking in a client-server architecture: client has message 'm' and function f. The task of client is to compute f(m). Due to computational expensiveness (maybe one of the reason) client sends encryption of message (say Enc(m)) and 'f' to the server. Server will compute function over encrypted message, that is, f(Enc(m)), and return the result to the client, that is, Enc(f(m)). Client will decrypt it Dec(Enc(f(m)), that is, f(m). Hence, client achieves f(m).  Let's understand HE with our daily life (Tea making process): Figure 1. Here m is message, Enc is encryption, f is function, and Eval in...
Read more

Fast Base Conversion and Its Application

Image
Fast Base Conversion (FBC) is a technique used to convert a number from one modulus space to another. For example, if we have 14 m o d     77 14 \mod 77  and want to convert it to x m o d     390 x \mod 390 , FBC is widely used. Mathematically, it can be represented as follows: Here, the above equation represents an integer x x  in modulus q q , and FBC converts this integer into the modulus space t t . The modulus q q  is the product of small coprime moduli (i.e., q = q 1 q 2 … q k q = q_1 q_2 \dots q_k ​ ), and x x  is an integer such that x ∈ [ 0 , q ) x \in [0, q) . We also note that q q  and t t  are coprime numbers. Here, we remark that it is not necessary for the above equation to produce the exact result for x x . Instead of x m o d     t x \mod t , it will provide x ′ m o d     t x' \mod t . Thus, the output of the above equation is as follows: FBC ( x , q , t )  =  x  +  A q  mod  t , where A ∈ [ 0 , k − 1 ] A \in [0,...
Read more

Brakerski-Fan-Vercauteren (BFV) Homomorphic Encryption

Image
Homomorphic encryption means computation over encrypted data without secret key.  How this is possible  ?? 😴 In this blog, we will explore the types of Homomorphic Encryption and demonstrate how computations can be performed on encrypted data without the secret key. In 2009, Gentry proposed Fully Homomorphic Encryption. In 2012, Brakerski proposed a leveled homomorphic encryption scheme that works over integer arithmetic, which later became known as the BFV scheme. BFV is an encryption scheme. Thus, as an encryption scheme, it is expected to be secure. To date, under certain conditions, it is assumed that the scheme is safe, and its security is based on the Learning With Errors (LWE) assumption.. Learning-with-error (LWE): Given a pair of a, b and the task is to recover secret key (s), such that b = a.s  + e  Here e is error mostly picked from gaussian distribution, and a, s are selected from Rq (known as ring module R) The above problem is HARD. The proof is not si...
Read more