Pseudorandom Number Generation and Stream Cipher

1.  The Use of Random Number 

1.1 Key Distribution : Two parties communicating by exchanging keys. In many cases nonces are used for handshaking to prevent replay attacks. 

1.2 Session Key Generation : Sometime a short key is needed during short period of time such as bank transactions. 

2. How to check Randomness

There are two ways to check randomness

2.1 Uniform Distribution : The frequency of occurrences of one and zero should be approximately equal.

2.2 Independence : No one subsequence in the sequence can be inferred  from the other.

3. How to Evaluate Random Number :

3.1 The function should be full period generating function. That is, the function should generate all the numbers from 0 through m-1 before repeating. 

3.2 The generated sequence should appear random.

3.3 The function should implement efficiently with 32 bit arithmetic. 

4. True Random Number Generation (TRNG) :

It takes an Input as source which is effectively random source or entropy source. This source may be the processing time, keystroke time, mouse moments and some environment dependable resources.

Fig. 1: True Random Number Generator

4.1 When to Use TRNG : Dealing with small bit's of number perform good whereas using large number of bit become tedious. 

5. Pseudo Random Number Generator(PRNG) :

In case of PRNG input is fix called as seed. It produces the output bit using the deterministic algorithm. Afterwards, for more complex output of algorithm is taken and fed as input to the algo to produce more bits or sequence of bits. 

Fig.2: Pseudo Random Number Generator

NOTE 1: If a person knows the seed value as well as algorithm then it is quite easy to generate the entire bit stream. 😒

6. Pseudo Random Function (PRF) :

It is used to produced a Pseudorandom string of bits of some fixed length. 

Input = Seed + Context Specific Values.

NOTE 2: What is Context Specific Values 😄 : User ID, Application ID, etc. 

Fig. 3: Pseudo Random Function

7. PRNG Requirement :

 Basically the requirement for a PRNG is that the generated bit stream appear random even though it is deterministic. 

Actually, there is no way to check bit stream is random or not but we apply some multiple test and on the behalf of multiple test we check the system satisfies the randomness requirement or not. 

Some test are : 

7.1 Uniformity : number of one's and zero's should be equal.

7.2 Scalability : if a test applicable on a sequence then it should also be applicable on subsequence. 

7.3 Consistency

7.4 Run Test or Frequency Test : How many time the random bit is generated and count the number of one's and zero's in every time. 

7.5 Mourer's Universal Statistical Test : The focus of this test is the number of bits between matching pattern. The purpose of the test is to detect whether or not the sequence can be significantly compressed without loss of information. A significantly compressible sequence is considered to be non random. 

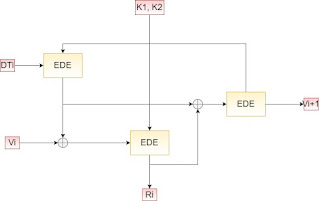
8. How to Generate Seed :

Figure 4 explains the generation of seed. The seed should be unpredictable or should be secure because if the seed is known to third person then it is quite very simple to break the message. so seed should be random or pseudo random. 

Fig. 4: Generation of Seed Input to PRNG

NOTE 3: Why PRNG is used when TRNG is already present ??👀 The reason behind is that when the stream cipher is present then TRNG is not practical.

9. Pseudo Random Number Generators

9.1 Linear Congruential Generators :

This algorithm is parameterized  with four numbers as follows:

m ---> modulus,  m>o

a  ---> multiplier,  0<a<m

c  ---> increment, 0<=c<m

Xo --> seed/starting value, 0<=Xo<m

So sequence of number {Xn}is obtained via the following iterative equation 

Xn+1 = (aXn + c) mod m

Here m, a, c, Xo are integers. 

The selection of values for a, c, and m is critical in order to generate the random number. 

NOTE 4: 1. A common criterion is that m be nearly equal to the maximum representable non negative integer. Thus, a value of m near to or equal to 2^31 typically chosen.

2. Since more than 2 billion possible choices for 'a', only a handful of multipliers pass all 3 tests. one such value of a = 7^5, which was originally selected for use in the IBM 360 family of computers. 

So, if the opponent knows that the linear congruential algorithm is being used and if the parameter are known (e.g. a = 7^5, c=0, m = 2^31 - 1), then once a single number is discovered, all subsequent numbers are known. 

9.2 Blum Blum Shub Generator :

First chose two large prime numbers Say P and Q and n = P.Q . Next, chose a random numbers, such that S is relatively prime to n; this is equivalent to saying that neither P nor Q is a factor of S. 

The BBS Generator produces a sequence of bits Bi according to following algorithm .

Fig.5: Blum Blum Shub Diagram

10. PRNG Using a Block Cipher

Two modes of operation i.e. CTR and OFB mode is widely used. In each case, the seed consists of two parts: the encryption key value and a value 'V' that will be updated after block of Pseudorandom numbers is generated. Thus, for AES-128, the seed consists of a 128 bit key and a 128 bit 'V' value. In CTR, the value V is incremented by 1 after each encryption. In the case of OFB, the value V is updated to equal the value of the preceding PRNG block. 

Fig. 6: PRNG Mechanism Based on Block Cipher

10.1 ANSI X9.17 PRNG

This technique involves a 112-bit key and three EDE (Encrypt- Decrypt-Encrypt) encryption for a total of nine DES decryption. This scheme is driven by two independent Inputs, the date and time and a seed produced by the generator that is distinct from the Pseudorandom produced by the generator.

If a pseudorandom number Ri were compromised, it would be impossible to deduce the Vi+1 from the Ri because an additional EDE operation is used to produced the Vi+1.

Figure 6 explains the algorithm, which makes use of triple DES for encryption. The ingredients are as follows - 

Input : Two Pseudorandom Inputs drive the generator. One is a 64 bit representation of the current date and time, which is updated on each number generation. The other 64 bit seed value; that is initialized to some arbitrary value and is updated during the generation process. 

Keys : The generation makes use of three triple DES encryption modules. All three make use of the same pair of 56- bit keys, which must be kept secret and are used only for Pseudo Random number Generation. 

Output : The output consists of a 64 bit Pseudo Random number and a 64 bit seed value. 

DTi --> Date/Time value at the beginning of ith generation stage. 

Vi --> Send value at the beginning of the generation stage, 

Ri --> Pseudo Random number produced by the ith generation stage.

K1, K2 --> DES kEYS USED FOR EACH STAGE. 

Then,

Ri = EDE([K1,K2],[Vi xor EDE([K1,K2], DTi)])

Vi+1 = EDE([K1,K2],[Ri xor EDE([K1,K2],DTi)])

Fig. 7: ANSI X9.17 Pseudo Random Number Generator

Here, EDE([K1, K2],X) refers to the sequence encrypt-decrypt-encrypt using two key triple DES to encrypt X. 

10.2 NIST CTR_DRBG :

Counter Mode deterministic random bit generator. 

The encryption algorithm used in DRBG may be 3DES with three keys or AES with a key size of 128, 192, or 256 bits. 

Four Parameter are associate with the algorithm.

-Output Block Length (OutLen)

-Key Length (KeyLen)

-Seed Length (SeedLen), and SeedLen = OutLen + KeyLen

-Reseed Integer (reseed interval) : Length of encryption key. It is the maximum number of output blocks generated before updating the algorithm with a new seed or also used to set the limit. 

Fig. 8: CTR_DRBG Functions

The Combination of K and V referred to as a seed. To start DRGB  operation initial value for K and V are needed, and can be chosen arbitrarily. These values are used to parameter for the CTR mode of operation to produce atleast SeedLen bits. In addition, exactly SeedLen bits must be supplied from what is referred to as an entropy source. Typically, the entropy source would be same form of TRNG.

11. True Random Number Generators 

Entropy Source : A TRNG used a non deterministic source to produce randomness. 

RFC 4086 lists the following possible sources of randomness that, withcare, easily can be used on a computer to generate true random sequences. 

Sound Video Input

Disk Drivers

NOTE 5: Comparison Between PRNG and TRNG.

Efficient - Produce more number in a short time

Deterministic - a given sequence of numbers can be reproduced at a later date if the starting point in the sequence its known. 

Table 1 : Comparison Between TRNG and PRNG.

	PRNG	TRNG
Efficiency	Very Efficient	Generally Inefficient
Determinism	Deterministic	Non Deterministic
Periodicity	Periodic	Aperiodic

12. Stream Cipher

The key is input to a pseudorandom bit generator that produces a stream of 8-bit number that are apparently random. The output of generator, called a keystream, is combined one byte at a time with the plaintext stream using the bitwise Xor operation. 

Fig. 9: Stream Cipher Diagram

There are some important consideration while designing a stream cipher. 

- The random encryption scheme should have a large period. A pseudorandom number generates uses a function that produces a deterministic stream of bits that eventually repeats. The longer the period of repeat the more difficult it will be to do cryptanalysis. 

- The keystream should approximate the properties of a true random number stream as close as possible means number of 0's and 1's should be equal. 

- The Output of the Pseudo Random number generator is conditioned on the value of the Input Key. 

13. RC4 :

- It is a stream cipher invented by Ron Rivest in 1987.

- RC stands for Ron's code

- Was kept secret until 1994 when it was published on cipher punks mailing list. 

13.1 Procedure : 

- Uses  an S- Array of Length 256 where S[0] = 0 to S[255] = 255.

- Has a key e.g. Key = "I Am The Key"

- Key Encoding using ASCII gives 73 32 65 77 32 84 72 69 32 75 69 89

- Has a key Array, K of Length 256 as well i.e. K[0] to K[255]. 

- Element of the key array are repeated i.e. 

K[0] = 73, K[11] = 88, K[12] = 73, K[13] = 32, K[255] = ?

13.2 Algorithm

13.2.1 Key Scheduling :

J=0

for i 0 to 256 do

    J = J+S[i] + K[i] % 256

    swap S[i] and S[j]

end for

13.2.2 Pseudo Random Generation Algorithm : 

Set i and J back to 0:

for i=i+1

     J = J+S[i] mod 256

    Swap S[i] and S[J]

    t = S[i] + S[j] mod 256

    Keystream = S[t]

end for

Encryption : CT = PT xor Keystream

Decryption : PT = CT xor Keystream

Example : Suppose S-Array of Length 8 whereby

[S0, S1, S2, S3, S4, S5, S6, S7] = [0,1,2,3,4,5,6,7]

Let the key be K = [3 1 4 1 5]

The K array thus is [K0, K1, K2, K3, K4, K5, K6, K7] = [3, 1, 4, 1, 5, 3, 1, 4]

So key scheduling 

J=0

for i=0 to 7 do

    J = J+ S[i] + K[i]%8

    Swap S[i]  and S[J]

end for

k-Array	---à	3	1	4	1	5	3	1	4
i	J	S0	S1	S2	S3	S4	S5	S6	S7
	0	0	1	2	3	4	5	6	7
0	3	3	1	2	0	4	5	6	7
1	5	3	5	2	0	4	1	6	7
2	3	3	5	0	2	4	1	6	7
3	6	3	5	0	6	4	1	2	7
4	7	3	5	0	6	7	1	2	4
5	3	3	5	0	1	7	6	2	4
6	6	3	5	0	1	7	6	2	4
7	6	3	5	0	1	7	6	4	2

So the New S-Array then become

    [3 5 0 1 7 6 4 2]

Let PT be [6 1 5 4]

Simplified Stream Generation (Pseudo- Random)

Set i and J back to 0

for i=i+1 to length of PT

    J=J+S[i]%8

    Swap S[i] and S[j]

    t = S[i] +S[j]%8

    Keystream  = S[t]

end for

i	J	t	Ks	S0	S1	S2	S3	S4	S5	S6	S7
0	0			3	5	0	1	7	6	4	2
1	5	3	1	3	6	0	1	7	5	4	2
2	5	5	0	3	6	5	1	7	0	4	2
3	6	5	0	3	6	5	4	7	0	1	2
4	5	7	2	3	6	5	4	0	7	1	2

Hence, 

Encryption : Ks = [1 0 0 2], PT = [6 1 5 4]

CT = PT xor Ks

 = [7 1 5 6]

Decryption : PT = CT xor Ks

PT = [6 1 5 4]