Block Cipher and the Data Encryption Standards

Outline

1. Block Cipher vs Stream Cipher

2. Block Cipher Designing Principles

3. Feistel Cipher

4. DES

1. Block Cipher and Stream Cipher

1.1 Block Cipher : In which a block of plaintext is treated as a whole and used to produce a ciphertext block of equal length. Typically a block size of 64 bit or 128 bits is used. 

Fig. 1. Block Cipher

1.2 Stream Cipher : In which data is encrypted one bit at a time.

Fig. 2. Stream Cipher

2. Block Cipher Design Principles

The main principles are defined below. This will be more cleared once you will study DES and Feistel Cipher. 

2.1 No. of Rounds : Greater the Number of rounds greater will be the difficulty to break. Generally, 16 rounds are considered. 

Note 1. Schneier observes that for 16 rounds DES, a differential cryptanalysis attach require 2^(55.1) operations whereas, Brute force requires 2^(55) operations. so if DES has 15 or less than 15 rounds differential cryptanalysis requires less effort that brute force. 

Differential cryptanalysis of DES requires 2^(47) chosen plaintext. if you have to work with is known plaintext then you must sort through a large quantity of known plaintext-ciphertext pairs looking for the useful ones. This brings the level of effort upto 2^(55.1). 

2.2 Design Function 'F' : The function 'F' should be non linear because non linear function are quite difficult to understand as well as break.

Note 2 : Strict Avalanche Criterion (SAC) : any output bit 'J' of S-box should change with probability 1/2 when any single input bit 'i' is inverted for all i, j.

Bit Independence Criterion (BIC) : output bit j and k should change independently when any single input bit i is inverted for all i, j, and k .

2.3 Key Schedule Algorithm : Select the subkeys to maximize the difficulty of deducing individual subkeys and the difficulty of  working back to main key.

3. Feistel Cipher

3.1 Motivation for Feistel Cipher 

As we know 'n' bit of plaintext will produce 'n' bit of ciphertext. so there are 2^(n) possible different plaintext. 

As we also know that for encryption to be reversible which means that decryption should also be possible. Now let's first discussed about reversible and irreversible mapping.

                           a. Reversible Mapping                                        b. Irreversible Mapping

                      Plaintext                Ciphertext                               Plaintext                Ciphertext

                           00                            11                                           00                            11

                           01                            10                                           01                            10

                           10                            00                                           11                            01

                           11                            01                                           10                            01

So in case of reversible mapping we can compute that for every unique plaintext it produce unique ciphertext. 

So if we wish to encrypt as well decrypt any message we have to focus on the reversible mapping. 

Now let's consider n=4 so there is total 2^(4) different plaintext i.e. {000,001,010,011,.....,110,111}.

As, when n=4 total number of different plaintext are 16, and the key length will be 4 x 2^(4).

Suppose n=m where m is any large integer, then key length will be mx2^(m). This is quite large so feistel cipher comes into existence. 

3.2 Feistel Cipher 

Feistel use the alternate substitution and permutation.

Feistel is a practical application of a proposal by claude shannon to develop a product cipher that alternates confusion and diffusion. 

Diffusion :  if we change a character of plaintext then several characters of ciphertext should change and vice versa.

Confusion : Each character of the ciphertext should depend on the several part of the key. 

The entire working process of feistel cipher is explained through Fig. 3

Fig. 3. Feistel Encryption and Decryption 

From Fig. 3. we can see than an encryption side

                LE(16) = RE(15)

And,        RE(16) = LE(15)%3CmxGraphModel%3E%3Croot%3E%3CmxCell%20id%3D%220%22%2F%3E%3CmxCell%20id%3D%221%22%20parent%3D%220%22%2F%3E%3CmxCell%20id%3D%222%22%20value%3D%22%22%20style%3D%22shape%3DorEllipse%3Bperimeter%3DellipsePerimeter%3BwhiteSpace%3Dwrap%3Bhtml%3D1%3BbackgroundOutline%3D1%3B%22%20vertex%3D%221%22%20parent%3D%221%22%3E%3CmxGeometry%20x%3D%22120%22%20y%3D%22540%22%20width%3D%2220%22%20height%3D%2220%22%20as%3D%22geometry%22%2F%3E%3C%2FmxCell%3E%3C%2Froot%3E%3C%2FmxGraphModel%3E Xor F(RE(15), K(16))

s

%3CmxGraphModel%3E%3Croot%3E%3CmxCell%20id%3D%220%22%2F%3E%3CmxCell%20id%3D%221%22%20parent%3D%220%22%2F%3E%3CmxCell%20id%3D%222%22%20value%3D%22%22%20style%3D%22shape%3DorEllipse%3Bperimeter%3DellipsePerimeter%3BwhiteSpace%3Dwrap%3Bhtml%3D1%3BbackgroundOutline%3D1%3B%22%20vertex%3D%221%22%20parent%3D%221%22%3E%3CmxGeometry%20x%3D%22120%22%20y%3D%22540%22%20width%3D%2220%22%20height%3D%2220%22%20as%3D%22geometry%22%2F%3E%3C%2FmxCell%3E%3C%2Froot%3E%3C%2FmxGraphModel%3E

So            RE(i) = LE(i-1) Xor F(RE(i-1),K(i))

For decryption side

               LD(1) = RD(0) = LE(16) = RE(15)

               RD(1) = LD(0) Xor F(RD(0),K(16))

               RD(1) = RE(16) Xor F(RE(15), K(16))

               RD(1) = [LE(15) Xor F(RE(15), K(16)] Xor F(RE(15),K(16))

In general, for i iteration of the encryption algorithm

               LE(i) = RE(i-1)

               RE(i) = LE(i-1) Xor F(RE(i-1), K(i))

or,           LE(i-1) = RE(i) Xor F(RE(i-1), K(i)) = RE(i) Xor F(LE(i), K(i))

Note 4 : The great advantage of feistel cipher is that it uses same structure for encryption and decryption but it has also some limitation like if  the value of 'F' function is weak then this structure is not accurate. 

3.3 Realization of Feistel Cipher

A. Block Size : Larger the block size, means greater security but this will reduced the encryption and decryption speed. 

Note 5 : Traditionally a block size of 64 bit has been considered a reasonable tradeoff and was nearly universal in block cipher.

B. Key Size : Larger the key increase security but again decrease the encryption and decryption speed. 

Note 6 : In general, 128 bits has become a common size.

C. No. of Rounds : Greater the round, greater the security but increase the complexity of algorithm that's why decrease the computation speed.

D. Round Function 'F' : Generally should be non linear because non linear function are quite difficult to understand.

E. Fast software Encryption/ Decryption : Deals with the speed of execution of the algorithm becomes a concern.

F. Ease of Analysis : Designing of your algorithm in that way no one can understand. 

4 Data Encryption Standards (DES) 

Before 2001 DES was the mostly used encryption scheme.

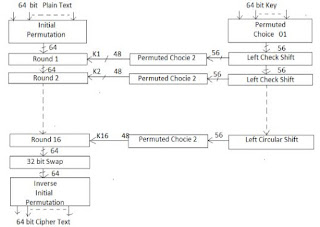
Fig. 4 shows the architecture of DES.

Fig. 4. DES

A 64 bit plaintext is given, then firstly it processed through the initial permutation block (which is also called P-block. P-block has no cryptographically significance but it just permutate the message for security perspective. Afterwards the message is passed through the round function (as discussed in Section 4.1) This round function gets the 48 bit key. 

In reality the bit size is also 64 bit but this 64 bit key is given to permutated choice which drops 8 parity bit and then it processed through left check shift. Further, Permutated choice 2 is also used because permutate the key prior to the key expansion. so again 8 bits are drop for parity.

Afterwards, round function 32 bit swap comes into picture which swap equally the 32 bit left and write swap and finally this bit is given to inverse initial permutation which is just reverse to initial permutation (also a part of P block). This inverse initial permutation will produce the ciphertext. 

4.1 Round Function 

In round block the 64 bit message is divided into equal left and right half, after that expansion (increase the number of bits i.e. 48 bit) is perform on the right half. The significance of expansion is that it is interpreted as for initial and final permutation means some bits from the input are duplicate at the output.

After that XOR operation is performed on the expansion and permutated choice. Further, the 48 bit result is given to the Substitution box (S-Box). Further S-box produce the 32 bit. This obtained 32 bit is XOR with next right half of round function (as shown in Fig. 5).

Fig. 5. Round Function

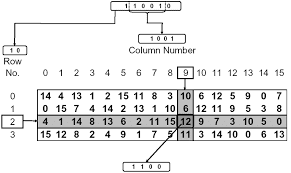
Note 7 : The 6 bit out of 48 bit works as an input for each S-Box means it will generate 8 S-box and it will produce the 4 bit out corresponding to each substitution box. In S-Box first two bits works for the row and rest middle 4 bits works for the column (as shown in Fig. 6).   

Fig. 6. S-Box

4.2 Strength of DES

A. The use of 56-bit Keys : For 56 bits total number of possible keys = 2^(56). Since this is large so if you apply brute force technique then it is quite difficult to perform but today we are working with supercomputers so we can easily perform this task.

B. The nature of Algorithm : It means design S-Box in that way so that it is difficult to break. 

C. Timing Attacks : A timing attack is one in which information about the key or the plaintext is obtained by observing how long it takes a given information to perform decryption on various ciphertexts.